С помощью этого руководства вы научитесь решать задачу с применением алгоритма имитации отжига, получите результаты решений и интерпретируете их. Для решения используется образ виртуальной машины «Квантовый симулятор» на мощностях CPU и предустановленный в образе сэмплер D-Wave.
«Квантовый симулятор» — это усовершенствованная реализация алгоритма имитации отжига. Симулятор предназначен для решения задач в постановке матрицы Quadratic Unconstrained Binary Optimization (QUBO). С его помощью вы можете решать сложные оптимизационные задачи, например: оптимизировать маршруты, логистические процессы, энергопотребление, планирование производственных процессов.
Вы будете использовать следующие сервисы:
«Виртуальные машины» — сервис, в рамках которого предоставляется виртуальная машина для развертывания симулятора.
«Публичные IP» — сервис для организации доступа к виртуальной машине через интернет.
Jupyter Server — серверное приложение, позволяющее запускать командные графические оболочки для интерактивных вычислений Jupyter Notebook и JupyterLab.
Шаги:
Перед началом работы
-
Если вы уже зарегистрированы, войдите под своей учетной записью.
Убедитесь, что для вашей учетной записи достаточно прав на проект. При необходимости настройте права или запросите их у администратора.
Запросите в технической поддержке пароль для квантового симулятора.
1. Разверните ресурсы в облаке
Создайте виртуальную машину со следующими параметрами:
Название — quantum-server.
Зона доступности — ru.AZ-1.
Образ — на вкладке Маркетплейс выберите «Квантовый симулятор».
Гарантированная доля vCPU — 30%.
vCPU, шт — 2.
RAM, ГБ: — 4.
Сетевой интерфейс — выберите тип Подсеть с публичным IP.
Публичный IP — оставьте Арендовать новый или выберите IP-адрес из списка арендованных.
Имя пользователя — cloud-user.
Метод аутентификации — Пароль.
Пароль — задайте пароль пользователя.
На виртуальной машине будет развернут Jupyter Server для работы с
.В строке созданной ВМ скопируйте и сохраните адрес из столбца Публичный IP: он потребуется для дальнейшей настройки.
Добавьте правило входящего трафика в группу безопасности SSH-access_ru.AZ-1:
Протокол
Порт
Тип источника
Источник
TCP
8888
IP-адрес
0.0.0.0/0
2. Подключитесь к Jupyter Server
Jupyter Server станет доступен через 5–7 минут после запуска виртуальной машины.
В браузере перейдите по адресу https://<public_ip>:8888, где <public_ip> — публичный IP-адрес ВМ quantum-server.
Если появится предупреждение о том, что подключение не защищено, добавьте сертификат сайта в доверенные по инструкции для вашего браузера.
В поле Password введите пароль, полученный в технической поддержке Cloud.ru.
Нажмите Log in.
Откроется страница с файлами симулятора.
Смените пароль Jupyter Server:
Откройте терминал: на верхней панели нажмите File → New → Terminal.
В терминале введите команду:
jupyter notebook passwordДважды введите новый пароль.
Создайте новый ноутбук:
На верхней панели нажмите File → New → Notebook.
В открывшемся окне выберите ядро Python 3.
3. Создайте матрицу
Импортируйте в проект библиотеки. Вставьте в ячейку ноутбука указанный ниже код и нажмите Shift + Enter.
import numpy as npfrom dwave.samplers import SimulatedAnnealingSamplerimport matplotlib.pyplot as pltГде:
numpy — библиотека для работы с массивами данных.
dwave.samplers — пакет с сэмплером D-Wave, в котором доступно несколько алгоритмов решения.
SimulatedAnnealingSampler — алгоритм имитации отжига из пакета D-Wave.
matplotlib — библиотека для визуализации.
Создайте матрицу со случайными значениями:
N = 10M = 10Q = np.random.uniform(low=-M, high=M, size=(N, N))Где:
N — размер матрицы;
M — диапазон значений;
Q — объект матрицы.
Чтобы убедиться, что матрица случайная, получите ее изображение:
plt.matshow(Q)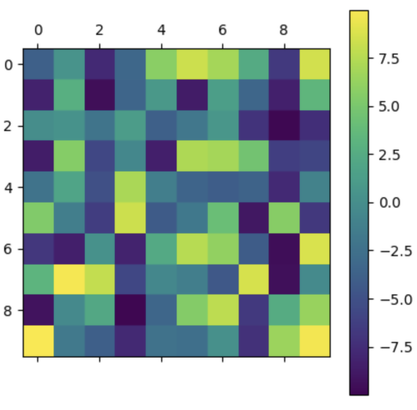
4. Запустите сэмплер
Запустите сэмплер D-Wave:
sampler = SimulatedAnnealingSampler()num_reads = 10num_sweeps = 10**3beta_range = [0.1, 4.2]beta_schedule_type = 'geometric'sample_set = sampler.sample_qubo(Q, num_reads=num_reads, num_sweeps=num_sweeps, beta_range=beta_range, beta_schedule_type=beta_schedule_type)Где:
sampler — объект решателя.
num_reads — количество запусков алгоритма.
num_sweeps — максимальное количество итераций алгоритма.
beta_range — расписание отжига, последовательность обратных температуре величин.
beta_schedule_type — тип интерполяции между точками.
Получите результаты:
print(sample_set)В результате отобразится таблица:
0 1 2 3 4 5 6 7 8 9 energy num_oc.0 1 1 1 0 1 0 0 0 0 1 -50.046614 11 1 1 1 0 1 0 0 0 0 1 -50.046614 12 1 1 1 0 1 0 0 0 0 1 -50.046614 13 1 1 1 0 1 0 0 0 0 1 -50.046614 14 1 1 1 0 1 0 0 0 0 1 -50.046614 16 1 1 1 0 1 0 0 0 0 1 -50.046614 18 1 1 1 0 1 0 0 0 0 1 -50.046614 19 1 1 1 0 1 0 0 0 0 1 -50.046614 15 0 1 0 0 1 1 0 0 1 1 -46.860889 17 0 1 0 0 0 1 0 0 1 1 -46.729231 1['BINARY', 10 rows, 10 samples, 10 variables]Где:
Столбцы от 0 до 9 показывают полученные решения. Каждое число в строке, 0 или 1, соответствует одной из переменных в векторе решения.
Столбец energy показывает значение функции \(E(x)\). Это число указывает, насколько эффективно решение с точки зрения достижения минимального значения функции — чем меньше число, тем лучше.
Столбец num_oc показывает, сколько раз конкретное решение было найдено.
Каждая строка в таблице представляет одну попытку решения задачи.
5. Выберите решение
Выберите решение одним из двух методов:
Чтобы получить конкретное решение, используйте метод record, отправив команду:
n = 9E = sample_set.record[n][1]x = sample_set.record[n][0]print("Energy is ",E)print("Solution is ",x)Где:
n — номер решения.
E — значение энергии, связанное с решением.
x — бинарный вектор, представляющий решение.
В результате отобразятся значения выбранного решения:
Energy is -50.046614387554584Solution is [1 1 1 0 1 0 0 0 0 1]Чтобы получить эффективное решение, используйте метод first, отправив команду:
x = sample_set.first[0]print("Energy is ",E)print("Solution is ",x)В результате отобразятся значения эффективного решения с точки зрения достижения минимального значения функции:
Energy is -50.046614387554584Solution is {0: 1, 1: 1, 2: 1, 3: 0, 4: 1, 5: 0, 6: 0, 7: 0, 8: 0, 9: 1}
Результат
Вы научились применять алгоритм имитации отжига для решения задач в постановке матрицы QUBO.